Attention: Here be dragons

This is the latest (unstable) version of this documentation, which may document features not available in or compatible with released stable versions of Godot.

Checking the stable version of the documentation...

矩阵与变换

前言

在阅读本教程之前，我们推荐你从头到尾阅读并且理解 向量数学 教程，因为本教程需要一点向量的知识。

这个教程介绍的是变换以及我们如何在 Godot 中使用矩阵表示它。这不是完整深入的矩阵指南。变换大多数时候被应用为平移、旋转、缩放，所以我们将会关注如何用矩阵表示这些变换。

虽然这个指南主要关注于 2D，使用 Transform2D 和 Vector2，但是 3D 中的工作方式也十分相似。

备注

正如之前的教程中提到的，要记住在 Godot 中，2D 的 Y 轴是向下的。这与学校里教的线性代数正好相反，在那里 Y 轴是向上的。

备注

这里的惯例是 X 轴用红色、Y 轴用绿色、Z 轴用蓝色。本教程中的颜色都遵循这个惯例，不过我们也在原点向量上使用蓝色。

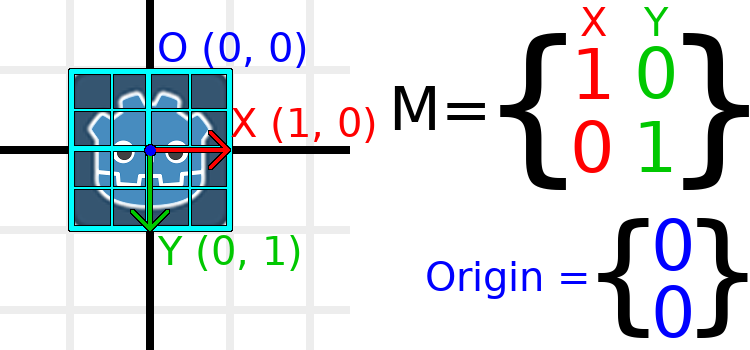
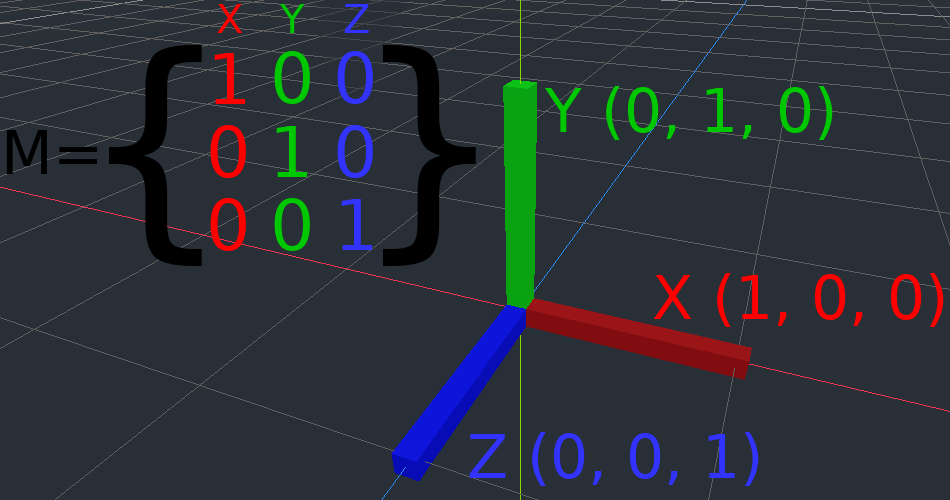
矩阵分量和单位矩阵

单位矩阵代表一个没有平移、没有旋转、没有缩放的变换。让我们开始看看单位矩阵以及它的分量如何与它的视觉表现相联系吧。

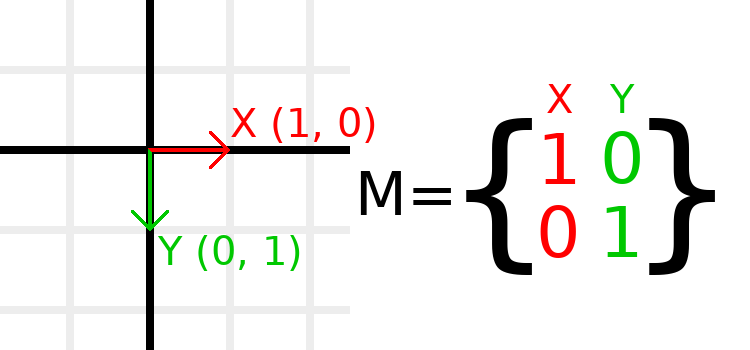
矩阵有行和列，变换矩阵对它们有特定的约定。

在上图中，我们可以看到红色的 X 向量由矩阵的第一列表示，绿色的 Y 向量则由第二列表示。改变列就会改变这些向量。我们将在接下来的几个例子中看到如何操作它们。

您不必担心直接操作行, 因为我们通常使用列. 然而, 你可以把矩阵的行看作是表示哪些向量有助于在给定的方向上移动.

When we refer to a value such as t.x.y, that's the Y component of the X column vector. In other words, the bottom-left of the matrix. Similarly, t.x.x is top-left, t.y.x is top-right, and t.y.y is bottom-right, where t is the Transform2D.

缩放变换矩阵

应用一个缩放是最容易理解的操作之一. 让我们开始吧, 把Godot logo放置于我们的向量之下, 这样我们可以直观得看出应用于这些对象上的效果:

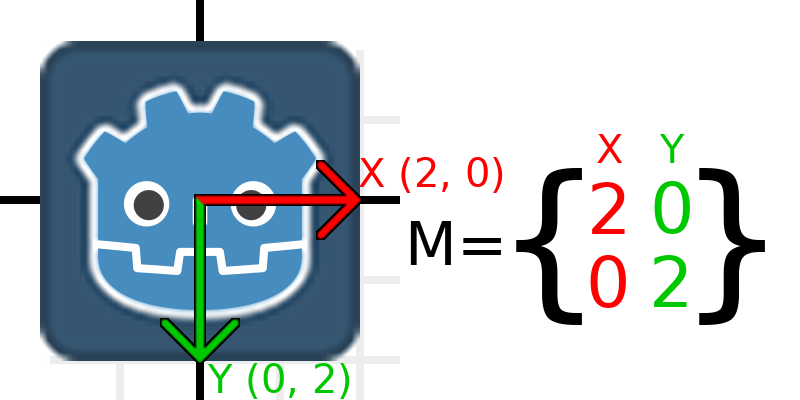
现在, 为了缩放矩阵, 我们唯一需要做的就是将每个矩阵分量乘以我们想要的缩放比例. 来将它缩放两倍吧,1乘以2变成了2,0乘以2变成了0, 所以我们最后得到了这个:

To do this in code, we multiply each of the vectors:

GDScriptC#

var t = Transform2D()
# Scale
t.x *= 2
t.y *= 2
transform = t # Change the node's transform to what we calculated.

如果我们想要回到它原来的尺度, 我们可以对每个分量乘以0.5. 这几乎就是缩放一个变换矩阵的全部了.

To calculate the object's scale from an existing transformation matrix, you can use length() on each of the column vectors.

备注

In actual projects, you can use the scaled() method to perform scaling.

旋转变换矩阵

我们将以与前面相同的方式开始, 在标识矩阵下使用Godot徽标:

举个例子，假设我们想顺时针旋转 Godot 标志 90 度。现在，X 轴指向右边，Y 轴向下。如果我们在头脑中旋转这些，我们就会在逻辑上看到，新的 X 轴应该向下，新的 Y 轴应该指向左边。

你可以想象, 你抓住了godot的图标和它的向量, 然后旋转它的中心. 无论你在哪里完成旋转, 向量的方向决定了矩阵是什么.

We need to represent "down" and "left" in normal coordinates, so means we'll set X to (0, 1) and Y to (-1, 0). These are also the values of Vector2.DOWN and Vector2.LEFT. When we do this, we get the desired result of rotating the object:

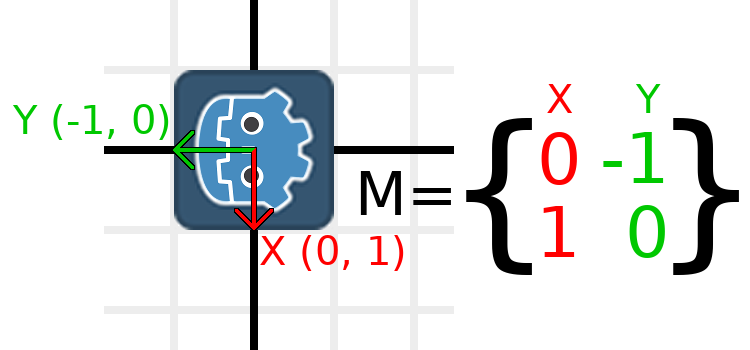
如果你很难理解上面的内容, 那就试试这个练习: 剪一个正方形的纸, 在上面画X和Y向量, 把它放在图表纸上, 然后旋转它并记下端点.

要在代码中执行旋转, 我们需要能够以编程方式计算值. 这幅图像显示了从旋转角度计算变换矩阵所需的公式. 如果这部分看起来很复杂, 别担心, 我保证这是你需要知道的最难的事情.

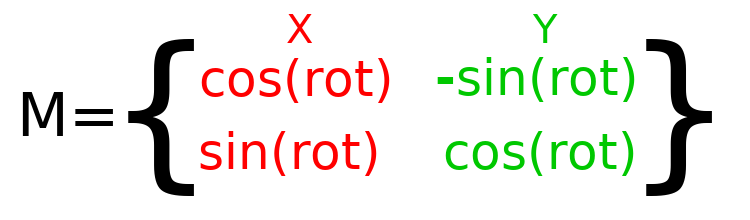
备注

Godot 用弧度表示所有的旋转，不用角度。完整转一圈是 TAU 或 PI*2 弧度，90 度的四分之一圈是 TAU/4 或 PI/2 弧度。使用 TAU 通常会让代码更易读。

备注

有趣的事实：在 Godot 中，不仅 Y 是朝下的，旋转也是顺时针的。这意味着所有的数学和三角函数的行为都与 Y 朝上的 CCW 坐标系相同，因为这些差异“相互抵消”了。你可以认为在这两个坐标系中的旋转都是“从 X 到 Y”。

In order to perform a rotation of 0.5 radians (about 28.65 degrees), we plug in a value of 0.5 to the formula above and evaluate to find what the actual values should be:

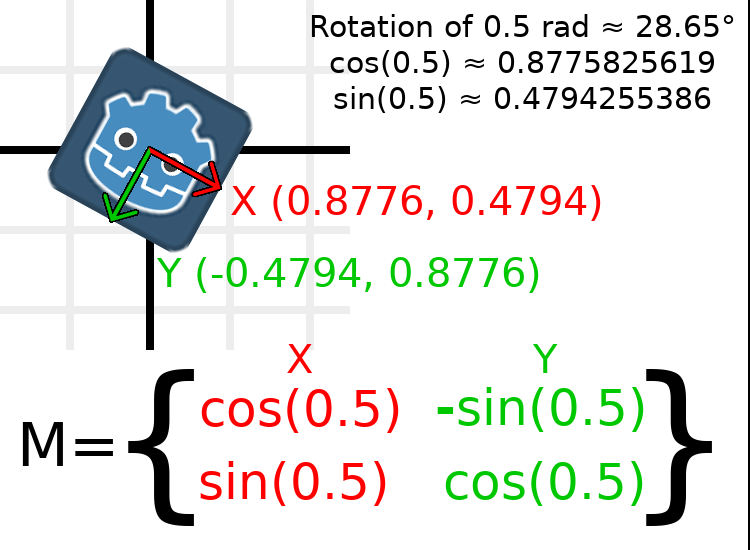
这是在代码中完成的方法（将脚本放在 Node2D 上）：

GDScriptC#

var rot = 0.5 # The rotation to apply.
var t = Transform2D()
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
transform = t # Change the node's transform to what we calculated.

To calculate the object's rotation from an existing transformation matrix, you can use atan2(t.x.y, t.x.x), where t is the Transform2D.

备注

In actual projects, you can use the rotated() method to perform rotations.

变换矩阵的基

So far we have only been working with the x and y, vectors, which are in charge of representing rotation, scale, and/or shearing (advanced, covered at the end). The X and Y vectors are together called the basis of the transformation matrix. The terms "basis" and "basis vectors" are important to know.

You might have noticed that Transform2D actually has three Vector2 values: x, y, and origin. The origin value is not part of the basis, but it is part of the transform, and we need it to represent position. From now on we'll keep track of the origin vector in all examples. You can think of origin as another column, but it's often better to think of it as completely separate.

Note that in 3D, Godot has a separate Basis structure for holding the three Vector3 values of the basis, since the code can get complex and it makes sense to separate it from Transform3D (which is composed of one Basis and one extra Vector3 for the origin).

变换矩阵的平移

Changing the origin vector is called translating the transformation matrix. Translating is basically a technical term for "moving" the object, but it explicitly does not involve any rotation.

让我们通过一个例子来帮助理解这一点。我们将像上次一样从恒等变换开始，但这次我们将记录原点向量。

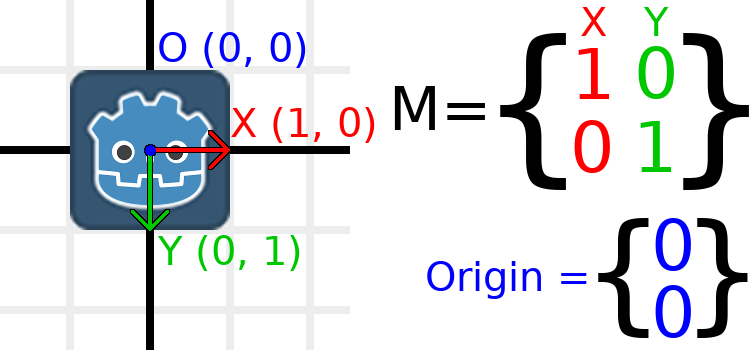
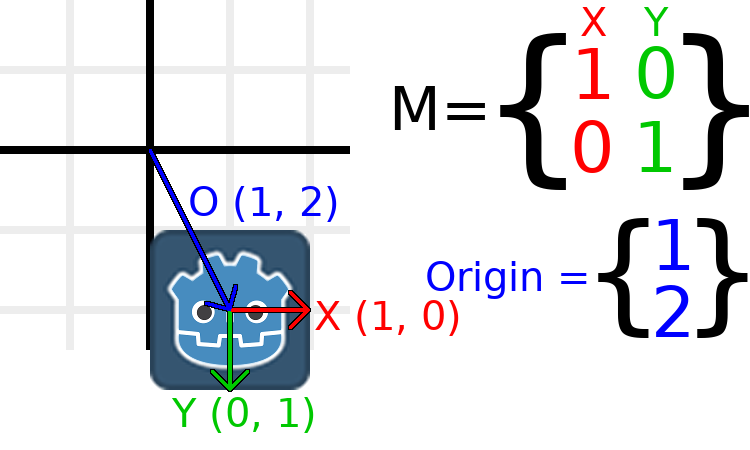
If we want to move the object to a position of (1, 2), we need to set its origin vector to (1, 2):

There is also a translated() method, which performs a different operation to adding or changing origin directly. The translated() method will translate the object relative to its own rotation. For example, an object rotated 90 degrees clockwise will move to the right when translated() with Vector2.UP.

备注

Godot 的 2D 使用基于像素的坐标，所以在实际项目中，你会想要转换成数百个单位。

融会贯通

We're going to apply everything we mentioned so far onto one transform. To follow along, create a project with a Sprite2D node and use the Godot logo for the texture resource.

让我们将平移设置为 (350, 150)，旋转设为 -0.5 rad，缩放设为 3。我把屏幕截图和重现代码都发出来了，但我鼓励您不看代码来尝试重现屏幕截图！

GDScriptC#

var t = Transform2D()
# Translation
t.origin = Vector2(350, 150)
# Rotation
var rot = -0.5 # The rotation to apply.
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
# Scale
t.x *= 3
t.y *= 3
transform = t # Change the node's transform to what we calculated.

剪切变换矩阵（高级）

备注

如果您只想了解如何使用变换矩阵，请随意跳过本教程的这一节。本节探讨变换矩阵的一个不常用的方面，目的是为了你建立对它们的理解。

Node2D provides a shearing property out of the box.

您可能已经注意到，变换的自由度比上述操作的组合要多。2D 变换矩阵的基在两个 Vector2 值中总共有四个数，而旋转值和缩放的 Vector2 只有三个数字。缺失自由度的高级概念称为剪切（Shearing）。

通常，您将始终拥有彼此垂直的基向量。但是，剪切在某些情况下可能很有用，了解剪切可以帮助您理解变换的工作原理。

为了直观地向您展示它的外观, 让我们在Godot徽标上叠加一个网格:

此网格上的每个点都是通过将基向量相加而获得的。右下角是 X + Y，而右上角是 X - Y。如果我们更改基向量，整个栅格也会随之移动，因为栅格是由基向量组成的。无论我们对基向量做什么更改，栅格上当前平行的所有直线都将保持平行。

例如, 让我们将Y设置为(1,1):

GDScriptC#

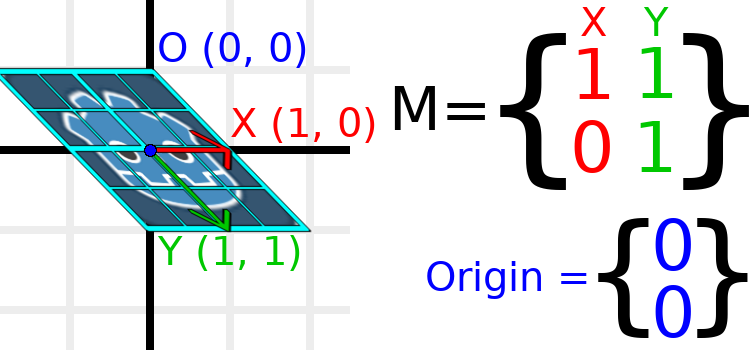
var t = Transform2D()
# Shear by setting Y to (1, 1)
t.y = Vector2.ONE
transform = t # Change the node's transform to what we calculated.

备注

不能在编辑器中设置Transform2D的原始值, 所以想要剪切对象, 必须使用代码.

由于向量不再垂直, 因此对象已被剪切. 栅格的底部中心(相对于自身为(0,1))现在位于世界位置(1,1).

对象内部坐标在纹理中称为UV坐标, 因此我们借用此处的术语. 要从相对位置找到世界位置, 公式为U*X+V*Y, 其中U和V是数字,X和Y是基向量.

栅格的右下角始终位于UV位置(1,1), 位于世界位置(2,1), 该位置是从X*1+Y*1(即(1,0)+(1,1)或(1+1,0+1)或(2,1)计算得出的. 这与我们观察到的图像右下角的位置相吻合.

同样, 栅格的右上角始终位于UV位置(1, -1), 位于世界位置(0, -1), 该位置是从X*1+Y*-1计算得出的,X*1+Y*-1是(1,0)-(1,1)或(1-1,0-1)或(0, -1). 这与我们观察到的图像右上角的位置相吻合.

希望您现在完全了解变换矩阵如何影响对象，以及基向量之间的关系以及对象的“UV”或“内部坐标”如何更改其世界位置。

备注

在Godot中, 所有变换数学运算都是相对于父节点完成的. 当我们提到 "世界位置" 时, 如果节点有父节点, 那么它将相对于节点的父位置.

如果你想要更多的解释，你可以查看 3Blue1Brown 关于线性变换的精彩视频：http://www.bilibili.com/video/BV1ys411472E?p=4

变换的实际应用

In actual projects, you will usually be working with transforms inside transforms by having multiple Node2D or Node3D nodes parented to each other.

However, it's useful to understand how to manually calculate the values we need. We will go over how you could use Transform2D or Transform3D to manually calculate transforms of nodes.

在变换之间转换位置

在许多情况下，您可能需要将某个位置转换为变换前或者变换后的位置。例如，如果您有一个相对于玩家的位置并想要查找世界（相对于玩家来说是父级）位置，或者如果您有一个世界位置并想知道它相对于玩家的位置。

We can find what a vector relative to the player would be defined in world space as using the * operator:

GDScriptC#

# World space vector 100 units below the player.
print(transform * Vector2(0, 100))

And we can use the * operator in the opposite order to find a what world space position would be if it was defined relative to the player:

GDScriptC#

# Where is (0, 100) relative to the player?
print(Vector2(0, 100) * transform)

备注

如果您事先知道变换位于 (0, 0) 处，则可以改用“basis_xform”或“basis_xform_inv”方法，这将跳过处理平移的过程。

相对于对象本身移动对象

一种常见的操作，尤其是在 3D 游戏中，是相对于自身移动对象。例如，在第一人称射击游戏中，当您按下 W 键时，您希望角色向前移动（-Z 轴）。

Since the basis vectors are the orientation relative to the parent, and the origin vector is the position relative to the parent, we can add multiples of the basis vectors to move an object relative to itself.

此代码会让对象向它自己的右边移动 100 个单位：

GDScriptC#

transform.origin += transform.x * 100

要在 3D 中移动，需要将“x”替换为“basis.x”。

备注

In actual projects, you can use translate_object_local in 3D or move_local_x and move_local_y in 2D to do this.

将变换应用于变换

关于转换, 需要了解的最重要的事情之一是如何将几个转换一起使用. 父节点的变换会影响其所有子节点. 让我们来剖析一个例子.

在此图像中, 子节点的组件名称后面有一个 "2", 以将其与父节点区分开来. 这么多数字可能看起来有点令人不知所措, 但请记住, 每个数字都会显示两次(在箭头旁边和矩阵中), 而且几乎一半的数字都是零.

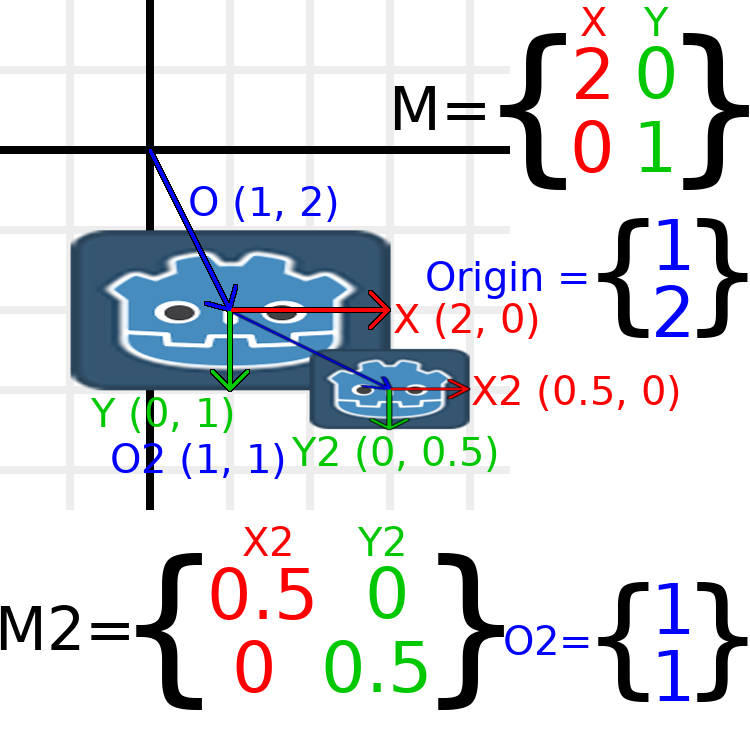
这里进行的唯一转换是父节点的比例为(2,1), 子节点的比例为(0.5,0.5), 两个节点都指定了位置.

All child transformations are affected by the parent transformations. The child has a scale of (0.5, 0.5), so you would expect it to be a 1:1 ratio square, and it is, but only relative to the parent. The child's X vector ends up being (1, 0) in world space, because it is scaled by the parent's basis vectors. Similarly, the child node's origin vector is set to (1, 1), but this actually moves it (2, 1) in world space, due to the parent node's basis vectors.

要手动计算子变换的世界空间变换, 我们将使用以下代码:

GDScriptC#

# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))

# Calculate the child's world space transform
# origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
var origin = parent.x * child.origin.x + parent.y * child.origin.y + parent.origin
# basis_x = (2, 0) * 0.5 + (0, 1) * 0
var basis_x = parent.x * child.x.x + parent.y * child.x.y
# basis_y = (2, 0) * 0 + (0, 1) * 0.5
var basis_y = parent.x * child.y.x + parent.y * child.y.y

# Change the node's transform to what we calculated.
transform = Transform2D(basis_x, basis_y, origin)

In actual projects, we can find the world transform of the child by applying one transform onto another using the * operator:

GDScriptC#

# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))

# Change the node's transform to what would be the child's world transform.
transform = parent * child

备注

当矩阵相乘时, 顺序很重要！别把它们弄混了.

最后, 应用身份变换始终不起任何作用.

如果您想了解更多信息，可以查看 3Blue1Brown 关于矩阵组成的精彩视频：http://www.bilibili.com/video/BV1ys411472E?p=5

求逆变换矩阵

The "affine_inverse" function returns a transform that "undoes" the previous transform. This can be useful in some situations. Let's take a look at a few examples.

将反变换乘以法线变换将撤消所有变换:

GDScriptC#

var ti = transform.affine_inverse()
var t = ti * transform
# The transform is the identity transform.

Transforming a position by a transform and its inverse results in the same position:

GDScriptC#

var ti = transform.affine_inverse()
position = transform * position
position = ti * position
# The position is the same as before.

这一切是如何在 3D 模式下工作的？

One of the great things about transformation matrices is that they work very similarly between 2D and 3D transformations. All the code and formulas used above for 2D work the same in 3D, with 3 exceptions: the addition of a third axis, that each axis is of type Vector3, and also that Godot stores the Basis separately from the Transform3D, since the math can get complex and it makes sense to separate it.

与二维相比, 有关平移, 旋转, 缩放和剪切在三维中的工作方式的所有概念都是相同的. 要缩放, 我们取每个分量并将其相乘；要旋转, 我们更改每个基向量指向的位置；要平移, 我们操纵原点；要剪切, 我们将基向量更改为不垂直.

如果您愿意, 最好尝试一下转换, 以了解它们是如何工作的. Godot 允许您直接从检查器编辑 3D 变换矩阵. 您可以下载此项目, 其中包含彩色线条和立方体, 以帮助在 2D 和 3D 中可视化 Basis 向量和原点: https://github.com/godotengine/godot-demo-projects/tree/master/misc/matrix_transform

备注

You cannot edit Node2D's transform matrix directly in Godot 4.0's inspector. This may be changed in a future release of Godot.

如果你想要更多的解释，你可以查看 3Blue1Brown 关于 3D 线性变换的精彩视频：http://www.bilibili.com/video/BV1ys411472E?p=6

表示 3D 中的旋转（高级）

2D 和 3D 变换矩阵之间最大的区别在于您如何在没有基向量的情况下自行表示旋转。

With 2D, we have an easy way (atan2) to switch between a transformation matrix and an angle. In 3D, rotation is too complex to represent as one number. There is something called Euler angles, which can represent rotations as a set of 3 numbers, however, they are limited and not very useful, except for trivial cases.

In 3D we do not typically use angles, we either use a transformation basis (used pretty much everywhere in Godot), or we use quaternions. Godot can represent quaternions using the Quaternion struct. My suggestion to you is to completely ignore how they work under-the-hood, because they are very complicated and unintuitive.

然而, 如果你真的想知道它是如何工作的, 这里有一些很棒的参考资料, 你可以按顺序跟随它们:

http://www.bilibili.com/video/BV1fx41187tZ

http://www.bilibili.com/video/BV1SW411y7W1

https://eater.net/quaternions